上下１ケタ～３ケタを検算する

まずは初めに結論を。一口で言うと。まとめ。要旨。

　簡易かつ手間の要らない検算方法。足し算をして得られた計算結果の、下１ケタ～下３ケタを検算すると、おおまかな正否が判明する。反対に、上１ケタ～上３ケタを検算しても、おおまかにわかる。計算ミスのメカニズムもある。

下１ケタ～下３ケタを検算する

　下の画像のような足し算しなくてはならないとします。

　

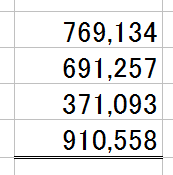
　で、電卓を叩いたら、下のような結果が出たとします。

　

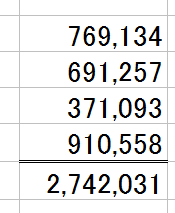
　合っているかどうか、検算してみましょう。

　一口で言うと、「下１ケタを計算すれば、おおまかにわかる」です。

　「４＋７＋３＋８」で、「２２」です。

　１０の位は、桁上がりがあるので、数字が違ってきます。しかし、１の位は桁上がりがないのですから、下１ケタの検算のように、１の位は「２」にならないといけないはずです。

　ここで瞬時に、この計算が間違っているのがわかります。

　桁数を上げると精度がよくなります。

　下２ケタの計算をすると…

　「３４＋５７＋９３＋５８」で、「２４２」です。

　１００の位のところは、先と同様、桁上がりがあるので数字は違っていても、１０の位は桁上がりがないので「４２」にならないといけないはず。

　でも、画像では「３１」なので、完全に間違っていると判明した次第です。

　ついでに、下３ケタもやってみましょう。

　「１３４＋２５７＋９３＋５５８」で、「１，０４２」。間違いですね。

　正しい計算結果は、「２，７４２，０４２」です。（わざわざ計算する必要はありません。）

　まとめます。

　下１ケタの計算で、１の位の正否が、

　下２ケタの計算で、１０の位までの正否が、

　下３ケタの計算で、１００の位までの正否がわかる、という塩梅です。

　全部を計算するのに比べたら、圧倒的に手間を減らして、計算結果を検算できると言う塩梅です。

　上の例では、見やすさという便宜上、４つの足し算ですが、売掛金のT字勘定のように、７個８個９個の足し算なら、かなりの威力を発揮します。

上１ケタ～上３ケタを検算する

　「下１ケタ～下３ケタ検算」の逆バージョンです。

　下の画像のような計算をしなくてはならず、で、電卓を叩いたら、下のような結果が出たとします。

　

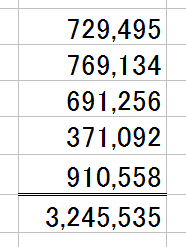
　合っているかどうか？を、上１ケタを足し算して検算してみましょう。

　「７＋７＋６＋３＋９」で、「３２」です。画像の計算結果も「３２」です。

　合っているかもしれません。

　上２ケタを足し算してみます。

　「７２＋７６＋６９＋３７＋９１」で、「３４５」です。画像は「３２４」です。アレレ。

　怪しくなってきました。

　上３ケタを足し算してみます。

　「７２９＋７６９＋６９１＋３７１＋９１０」で、「３４７０」です。画像は「３２４５」。うーむ。

　この時点で、この計算が間違っているのが、判明しました。

　ちなみに、正解は「３，４７１，５３５」です。（わざわざ計算する必要はありません。）

　このやり方も、“だいたいわかる”方式です。

　桁上がりがあるので、一番最後の数は違っていても、桁上がりのない位は、「同じ数字」にならないといけません。で…、

　上１ケタの計算で、最高位の正否が、

　上２ケタの計算で、次順位までの正否が、

　上３ケタの計算で、上３位までの正否が、検算できる塩梅です。

　全部を計算するのに比べたら、圧倒的な手間要らずで、計算結果を検算できます。

中ほど、間違えやすい－計算ミスのメカニズム

　下の画像を見てください。

　

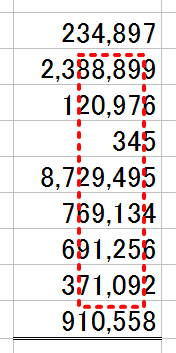
　いちばん最初の「２３４，８９７」とか、最後の「９１０，５５８」は、まず、打ち間違えることはないです。

　で、下１ケタの「７、９、６、５、５…」のところも、あんまり打ち間違えないです。

　同様に、上１～２ケタの「２、２３、１、３、８７…」も、打ち間違えることは少ないはず。

　なぜかというと、“見やすい”から。

　赤線で囲んだ、“中ほどの数字が固まっているところ”ほど、打ち間違え・見間違えが発生しやすいところです。

　なぜなら、周りを数字で囲まれているため、“見にくい”から。

　中ほど間違えやすいです。電卓への入力の際は、意識を（間違えるよ）とか（落ち着けよ）的に、切り替えてみてください。

　ちょっと意識するだけで、計算ミスはかなり減ります。

　なお、検算のコツ以上に、ミス率は、電卓の品質で大きく変わります。ぶっちゃけ、いちばん変わるところです。

　能率はお金で買えます。簿記（FPなど電卓を使う試験）の勉強を１００円ショップのペラペラ計算機でしているなら、「簿記検定試験の計算機(電卓)選び」を読むことを勧めます。

　読むのがメンドウなら、「売れ筋の電卓は、結局なに？」を参考にして買い換えましょう。計算ミスが驚くほど少なくなります。

★みんなとシェアする

△