奇数が偶数なら、偶数

まずは初めに結論を。一口で言うと。まとめ。要旨。

　奇数が、偶数個しかない場合の足し算は、必ず偶数になります。奇数の数を数えるだけで、大雑把な検算が可能です。そのほか、「奇数が偶数なら、偶数」や「奇数と偶数なら、奇数」など。

奇数が偶数なら、偶数

　結構な有用度です。

　↓のような、売掛金の集計によくある『おなじみ足し算』をするとします。

　

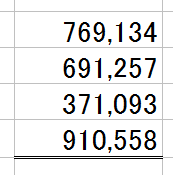
　で、電卓を叩いた結果、「2,742,031」でした、と。

　

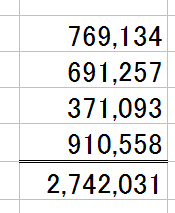
　↑の計算結果が正しいかどうかは、カンタンに確かめられます。

　結論から言うと、「奇数が偶数個なら、計算結果は“偶数”だ」という塩梅です。

　奇数の数を数えましょう。

　

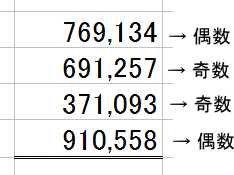
　奇数は、２つです。

　

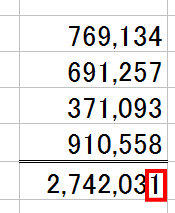
　奇数が２つ＝偶数なら、計算結果は“偶数”になるのに、なってません。

　だから、計算結果の「2,742,031」は、間違っているという塩梅です。答えは、「2,742,042」です。

　いちいち、長ったらしい計算のすべてをやり直さなくても、「数を数えるだけ」で、おおまかな検算ができるのでした。

　結構、強力な技だと思います。

偶数だけなら偶数

　まあまあの有用さです。

　こういう足し算をしなくてはいけなくて、電卓を叩いた結果、下の画像になったとします。

　

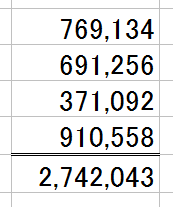
　↑の計算結果が正しいかどうかは、同じような塩梅で、カンタンに確かめられます。

　一口で言うと、「偶数だけの計算は、答えも偶数だ」です。

　

　全部偶数の足し算です。

　

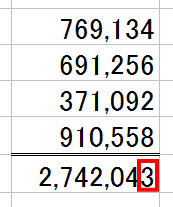
　計算結果は奇数になっているので、これまた、間違いだとスグに判明するわけです。

　正直、使用頻度の高い検算ではありませんが、頭の片隅に置いておけば、ちょっとしたT字勘定の集計に役に立つかと思います。

奇数と偶数なら、奇数

　ちょっと手間がかかるので、有効ではありません。

　「奇数と偶数の足し算なら、奇数になる」という、検算方法もあります。

　「３＋２」なら「５」の奇数です。このように、奇数と偶数の足し算の計算結果は、奇数にならなくてはならず、偶数になってたら、即間違いと判定できるという塩梅です。

　しかし、「３＋２」なら「５」のような、単調な計算なら苦労しないわけです。

　大方は、「１２３＋４９０＋４，０９８＋２１２，２１４」といった風な、長い足し算となるわけです。

　例のように、偶数と奇数が固まってくれたら、スグに検算できます。「奇数＋（偶数＋偶数＋偶数）」なので、答えは、奇数にならないといけないですね、

　しかし、試験問題は、計ってか計らいでか、偶数・奇数が入り混じってます。

　このため、いちいち、偶数と奇数の数を集計しないといけません。

　こんな余計な作業こそ、ミスのもと。この検算方法は、ごく少ない集計の検算として、使ってみてください。

　なお、検算のコツ以上に、ミス率は、電卓の品質で大きく変わります。

　能率はお金で買えます。簿記（FPなど電卓を使う試験）の勉強を１００円ショップのペラペラ計算機でしているなら、「簿記検定試験の計算機(電卓)選び」を読むことを勧めます。

　読むのがメンドウなら、「売れ筋の電卓は、結局なに？」を参考にして買い換えましょう。計算ミスが驚くほど少なくなります。

★みんなとシェアする

△