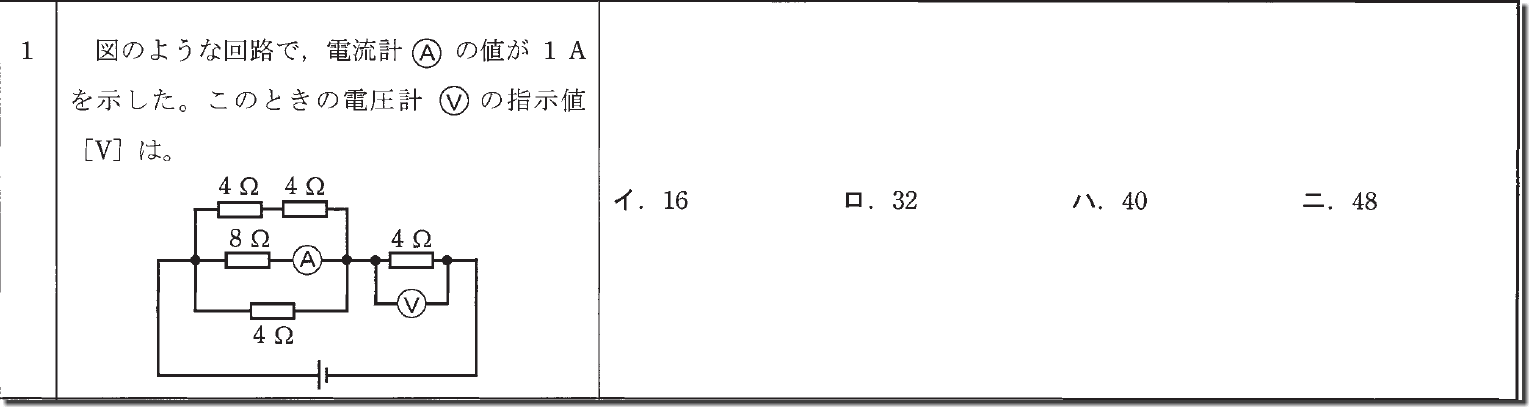
第1問は、理論問題で定番の計算問題です。

基本的な公式と決まり事を覚えておけば、文系ド素人でも取れます。

本問のような抵抗の計算問題は、まず、「どこを求めるのか？」を見極めましょう。

でないと、無駄な計算をしてしまい、たとえば、並列回路の合成抵抗を計算したりで、混乱しかねません。

本問は、「右側部分の4Ωの抵抗にかかっている電圧」を求めるわけです。

「V=IR」です。Rは4Ωと判明していますから、残るは「I」を求めればいいわけです。

当該Iを、左側の並列回路で求めればよい、という次第です。

解説

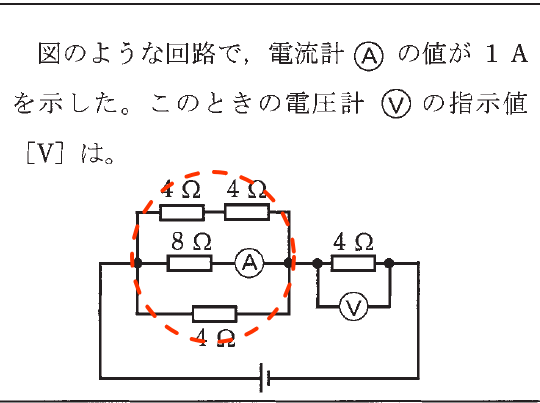
本問のキーは、「並列回路」にかかっている電圧は同じ、であることです。

上の画像の赤点線で囲んだ並列回路の、真ん中の「8Ω」には、「1A」流れています。

ということは…、

「V=IR」ですから、「V＝8*1」で「8V」がかかっているわけです。

当該「8V」は、並列回路の上の「4Ωと4Ω」のところにもかかっています。

直列なので足せばいいだけなので、「8Ω」に「8V」な塩梅です。

電流（I）は、「I=V/R」なので、「8/8」で「1A」となります。

並列回路の下のところも同じ要領で…、

「I=V/R」で「8/4」で「2A」となります。

これで、並列回路に流れるAがわかりました。

上から「1+1+2」で、合計「4A」です。

当該「4A」が出たら、答えは出たようなものです。

「4A」が「4Ω」のところに流れていますから…、

「V＝IR」で、「V=4*4」の「16V」となります。

んなもんで、答えは「イ」となります。

まとめ

本問は、基本的な計算問題で、「オームの法則」と「並列接続には同じ電圧」さえ知っていれば、問題が解けます。

本試験では、おおむね第1問目に、本問のような計算問題がでます。

電気理論には、文系ド素人には厳しい問題が多々あります。

ですから、本問のような、少々の公式知識と、掛け算と足し算で解ける問題は、実に貴重です。

何度も練習して、必ず解けるようになっておきます。

また、本試験では、本問と似たような計算問題が出るので、オームの法則の使い方などを、本問でしっかり練習しておきましょう。

なお、勉強方法等は「第２種電気工事士の独学」を…、

独学向け教材については、「筆記試験の教材」と「技能試験の教材」をばお目汚しください。

第2問は、「電気の基本的な知識」を問う問題です。

本問を解くには、電気の常識「電気は流れやすいところに流れる」を知っていることが必要です。

本問は、解説を読めば（なーんだ）の問題なのですが、緊張する本試験で本問が出たら、かなりの受験生が混乱して、上手に解けないはずです。

こういう問題の存在を、しっかり頭に叩き込んでおきましょう。

解説

スイッチ１（S1）を閉じると、電気は、下のスイッチのところを流れます。

反対に言えば、上記画像の赤点線で囲んだ「上側の30Ωの抵抗」のところに、電気は流れません。

先に言ったように、「電気は流れやすいところに流れる」からです。

んなもんで、「上側の30Ωの抵抗」は、無視できるという塩梅です。

さて、スイッチ２（S2）ですが、問題の指示では、「スイッチ２は開く」とあります。

要は、「電路がつながってない」わけで、電気は流れません。

んなもんで、上記画像の赤点線で囲んだ30Ωのところに電気は流れず、従って、無視できるという寸法です。

説明

ここまで到達すれば、後は、足し算だけです。

上記画像のように、赤点線部分は無視で、黒点線部分に電気が流れることになります。

本問だと、抵抗が直列で接続されていることになるので、「30Ω＋30Ω」で「60Ω」となり、答えは「ロ」と相なる次第です。

まとめ

本問は、基本的な電気知識を問う問題です。

まあ、直列接続の合成抵抗の出し方がわからない人はそういないでしょう。

ただ、先述したように、本問は『出題がシンプルなだけ、難しく考え過ぎて、自滅する』傾向があります。

本試験では、こういうシンプルな問題もあると、頭の片隅に置いていてください。

本問も、文系ド素人でも取れる数少ない電気理論の問題です。

何度も練習して、必ず解けるようになっておきます。

なお、勉強方法等は「第２種電気工事士の独学」を…、

独学向け教材については、「筆記試験の教材」と「技能試験の教材」をばお目汚しください。

第3問は、「電気抵抗」の公式を使った計算問題です。

「電気抵抗」の公式とは…、

R＝ρL/S

…です。

Rは抵抗（たぶん、レジストのR）で、「ρ」は「ロー」で抵抗率、Lは長さ（たぶん、レングスのL）、Sは断面積（たぶん、スクエアのS）となっています。

本公式は、銅銅導の太さが「断面積」の場合に、使います。

なお、銅銅導が「直径」の場合は…、

R＝4ρL/πD²

…となります。

「D」は直径です。（たぶん、ダイアメタ：diameterのDです。）

解説

本問は、先の公式で計算するのですが、実は、「絶縁電線の許容電流」の表を憶えていると、計算せずに解けます。

ポイントは、問題文には、「ほにゃららに近い銅材質の銅導線」となっているところで、「近い数字」ならよいという塩梅で、反対に言えば、「一致しなくてもよい」といった次第です。

んなもんで、「絶縁電線の許容電流」の表でざっくり求めてよい、という次第です。

問題文の「直径2.6mm、長さ10mの銅導線」を、当該表に照らし合わせると、許容電流値は「48A」です。

当該許容電流値「48A」に“近い”のは、「より線の5.5mm²」の「49A」となります。

問題文の銅導線は「10メートル」で、選択肢「ロ」のそれも同じ「10メートル」なので、長さも問題ありません。

んなもんで、答えは「ロ」となります。

説明

先の公式を当てはめて、答えを求めることができますが、面倒なので各自でしたい人だけしてください。

なお、「イ」の選択肢は、「直径」なので、「R＝4ρL/πD²」で計算します。

「ハ」も、「直径」なので、「R＝4ρL/πD²」で計算します。

「ニ」は、「断面積」なので、「R＝ρL/S」で計算します。

計算機を叩いてアレしてください。

まとめ

本問は、電気抵抗の公式を使わずとも、「絶縁電線の許容電流」の表で解くことができます。

試験的に言えば、公式の計算は面倒すぎるので、当該「絶縁電線の許容電流」の表で解くのがベターかと思います。

数字さえ憶えれば本問は解けるので、暗記に勤めましょう。

なお、先の公式は、単独で出題される公算が「大」なので、文系ド素人は、必ず憶えましょう。

文系ド素人でも取れる数少ない電気理論の問題なので、「表で解く」「公式で解く」で何度も繰り返してして、必ず解けるようになっておきます。

なお、勉強方法等は「第２種電気工事士の独学」を…、

独学向け教材については、「筆記試験の教材」と「技能試験の教材」をばお目汚しください。